Розв’язування логарифмічних нерівностей
УРОК 61
Тема. Розв’язування логарифмічних нерівностей
Мета уроку. Формування умінь учнів розв’язувати логарифмічні нерівності
І. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, що виникли в учнів при виконанні цих завдань.
II. Сприймання і усвідомлення розв’язування логарифмічних нерівностей (які розв’язуються введенням нової змінної)
Приклад 1. Розв’яжіть нерівність log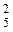 х – log5 x > 2.
х – log5 x > 2.
Нехай log5х = у, тоді отримаємо нерівність
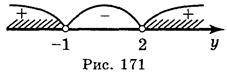
Розв’яжемо отриману нерівність методом інтервалів (рис. 171): y 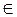 (-
(-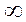 ; -1)
; -1)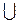 (2; +
(2; + ).
).
Враховуючи заміну матимемо:
1) log5 x < -1; log5 x < log5 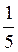 ;
; 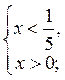 х
х 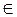
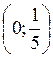 ;
;
2) log5 x > 2; log5 x > log525; 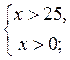 x
x 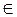 (25; +
(25; +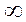 ). Отже,
). Отже, 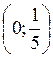
 (25; +
(25; +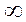 ) – розв’язок даної нерівності.
) – розв’язок даної нерівності.
Відповідь: 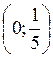
 (25; +
(25; + ).
).Приклад 2. Розв’яжіть нерівність 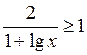 .
.
Нехай lg x = у, тоді матимемо нерівність
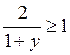 ; у? 1;
; у? 1; 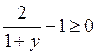 ;
; 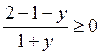 ;
; 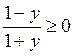 .
.
Розв’яжемо отриману нерівність методом інтервалів (рис. 172): у 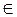 (-1; 1].
(-1; 1].
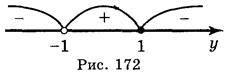
Враховуючи заміну, отримаємо -1 < lg x 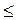 1.
1.
Тоді 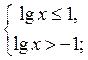
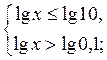
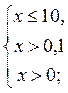 отже, х
отже, х 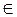 (0,1; 10] (рис. 173).
(0,1; 10] (рис. 173).
Відповідь: (0,1; 10].

III. Формування умінь розв’язувати логарифмічні нерівності
Виконання вправ № 59 (10), 60 (15).
IV. Сприймання і усвідомлення розв’язування логарифмічних (комбінованих) нерівностей методом інтервалів
Приклад 1. Розв’яжіть нерівність (3х – 6)log0,5 x > 0.
Розв’язання
Нехай у = (3х – 6) log0,5 x, у > 0.
Область визначення функції у: х > 0.
Знайдемо нулі функції: (3х – 6) – log0,5 x = 0;
3х – 6 = 0, log0,5 х = 0;
Х = 2, х = 1.
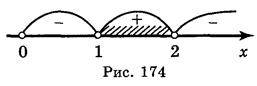
Розіб’ємо область визначення функції на проміжки точками 2 і 1 і знайдемо знаки функції на утворених проміжках (рис. 174). Отже, х 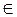 (1; 2).
(1; 2).
Відповідь: (1; 2).
Приклад 2. Розв’яжіть нерівність log x-3(х – 1) < 2.
Розв’язання
Нехай у = log x-3(х – 1) – 2 і у < 0. Область визначення функції знаходимо із системи: 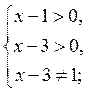
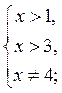 х
х 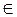 (3; 4)
(3; 4) 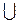 (4; +
(4; +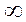 ).
).
Знайдемо нулі функції: log x-3(х – 1) = 2; х – 1 = (х – 3)2; х – 1 = х2 – 6х + 9; х2 – 7х + 10 = 0; х = 5, х = 2. х = 2 – не входить в область визначення функції. Перевіркою переконуємося, що х = 5 – нуль функції.
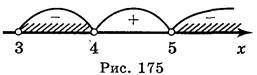
Розіб’ємо область визначення функції на проміжки точкою 5 та знайдемо знаки функції на утворених проміжках (рис. 175).
Отже, х 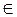 (3; 4)
(3; 4) 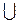 (5; +
(5; +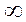 ).
).
Відповідь: (3; 4) 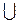 (5; +
(5; +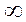 ).
).
V. Формування умінь розв’язувати логарифмічні нерівності
Виконання вправ № 59 (8), 60 (12).
VI. Сприймання і усвідомлення графічного способу розв’язування логарифмічних нерівностей
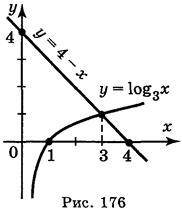
Приклад. Розв’яжіть нерівність log3 x < 4 – х графічно.
Розв’язання
Побудуємо графіки функцій у = log3 x і у = 4 – х в одній системі координат. Графіки перетинаються в точці А з абсцисою х = 3 (рис. 176).
Із рисунка видно, що множина розв’язків нерівності log3 x < 4 – х є проміжок (0; 3].
Відповідь: (0; 3].
VII. Підведення підсумків уроку
VIII. Домашнє завдання
Підготуватися до тематичної контрольної роботи. Вправи № 59 (7; 9), 60 (11).