Кут між мимобіжними прямими
Урок 53
Тема. Кут між мимобіжними прямими
Мета уроку: формування поняття кута між мимобіжними прямими, а також вмінь учнів знаходити кути між мимобіжними прямими.
Обладнання: стереометричний набір, моделі куба, тетраедра, прямокутного паралелепіпеда.
Хід уроку
II. Перевірка домашнього завдання
В кінці уроку збираються учнівські зошити для перевірки їх ведення і виконання домашнього завдання.
III. Сприйняття й усвідомлення нового матеріалу
Введемо поняття кута між прямими в просторі.
Якщо дві прямі перетинаються,
Якщо прямі перпендикулярні, то величина кута між цими прямими дорівнює 90°.
Кут між паралельними прямими вважають таким, що дорівнює 0°. Слід зазначити, що кут між прямими – це не геометрична фігура, це – величина.
Розв’язування вправ
1. ABCDA1B1С1D1 – куб. Знайдіть кут між прямими:
А) АВ1 і AD1; б) АВ1 і AD; в) АВ1 і АВ; г) АС і AC1.
(Відповідь: а) 60° ; б) 90° ; в) 45° ; г) arcsin 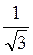 )
)
2.
3. ABCDA1B1C1D1 – прямокутний паралелепіпед, в якому АВ = а, AD = b, АА1 = с. Знайдіть кут між прямими:
А) А1В і АВ; б) A1D і AD; в) BD і АВ; г) ВА1 і DA1.
(Відповідь, a) arctg 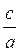 ; б) arctg
; б) arctg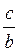 ; в) arctg
; в) arctg 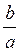 ; г) arccos
; г) arccos 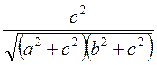 )
)
Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні відповідно даним мимобіжним прямим.
Кут між мимобіжними прямими, як і між прямими однієї площини, не може бути більше 90°. Дві мимобіжні прямі, які утворюють кут в 90°, називаються перпендикулярними.
1. Покажіть перпендикулярні мимобіжні прямі в оточенні.
2. Дано зображення куба (рис. 275). Знайдіть кут між мимобіжними прямими а і b.
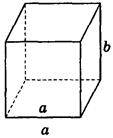
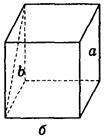
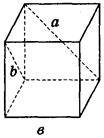
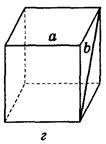
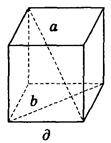
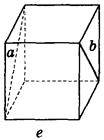
Рис. 275
(Відповідь, а) 90°; б) 45° ; в) 60°; г) 90°; д) 90°; е) 90°)
3. Дано куб ABCDA1B1C1D1. Доведіть, що АВ1 CD1.
CD1.
4. Пряма SA перпендикулярна до сторін АВ і АС трикутника АВС. Знайти кут між прямими SA і ВС. (Відповідь. 90°)
5. Точки К і М середини ребер АВ і DC трикутної піраміди DABC, кожне ребро якої дорівнює а. Доведіть, що KM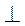 АВ. Знайдіть довжину відрізка KM.
АВ. Знайдіть довжину відрізка KM.
(Відповідь. 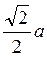 )
)
6. Знайдіть кут між мимобіжними діагоналлю грані куба і діагоналлю куба.
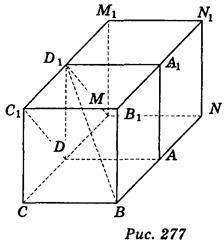
Знайдемо кут між діагоналлю ВD1 куба і діагоналлю DC1 грані куба (рис. 276). Добудуємо до даного куба куб ADMNA1D1M1N1 (рис. 277), тоді кут між прямими BD1 і DC1 дорівнює куту між прямими BD1 і D1M. Нехай АВ = а; тоді D1M =  А, AD1 =
А, AD1 = 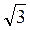 A, ВМ =
A, ВМ = 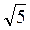 А.
А.
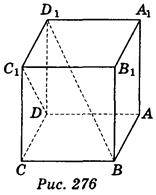
Із? BD1M маємо:
ВМ2 = DB2 + D1M2 – 2AD1 – D1M cosBD1M, або
5а2 = 2а2 + 3а2 – 2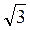 А –
А –  A cos BD1M;
A cos BD1M;
5а2 = 5а2 – 2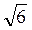 А2 cos <BD1M;
А2 cos <BD1M;
2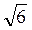 А2 cos <BD1M = 0;
А2 cos <BD1M = 0;
Cos <BD1M = 0;
<BD1M = arccos 0 = 90°.
Відповідь. 90°.
7. Довести, що кут між мимобіжними прямими не залежить від вибору прямих, що перетинаються.
Враховуючи означення кута між мимобіжними прямими, можна дати узагальнене означення перпендикулярності прямої і площини, ознаки перпендикулярності прямої і площини, теореми про три перпендикуляри.
Якщо пряма перпендикулярна до площини, то вона перпендикулярна до будь-якої прямої, що лежить у цій площині.
Якщо пряма перетинає площину, перпендикулярна до двох прямих цієї площини, що перетинаються, то вона перпендикулярна до площини.
Узагальнена теорема про три перпендикуляри
Будь-яка пряма на площині, перпендикулярна до проекції похилої на цю площину, перпендикулярна і до похилої. І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
1. Задача № 30 із підручника (с. 56).
2. Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що перетинаються, то вона перпендикулярна до площини. Довести.
3. Задача № 33 із підручника (с. 56).
4. Дано куб ABCDA1B1C1D1. Доведіть, що АС1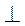 BD.
BD.
5. ABCD – ромб (рис. 278), пряма SO перпендикулярна до площини АВС. Доведіть, що SC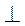 BD.
BD.
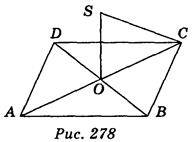
6. SABC – трикутна піраміда, всі ребра якої рівні. Доведіть, що SA ВС.
ВС.
§4, п. 31; контрольне запитання № 14; задача № 32 (с. 56).
Запитання до класу
1) Що називається кутом між мимобіжними прямими?
2) Чи залежить кут між мимобіжними прямими від вибору прямих, які перетинаються?
3) Сформулюйте узагальнене означення перпендикулярності прямої і площини.
4) Сформулюйте узагальнену ознаку перпендикулярності прямої і площини.
5) Сформулюйте узагальнену теорему про три перпендикуляри.
